

Applying this to − 3 4 , we see that it Rule, which tells us that any power can be expressed as the reciprocal of a power with the same base but opposite exponent: Notice that inside the big parentheses, we have a fraction to the power of − 1. Raising a power to a further power is done by writing the base with an exponent equal to the product of the two exponents:īy writing the exponent − 2 as ( − 1 ) ⋅ 2, we can work backward from this Recall the power of a power rule, which tells us that We start by transforming the negative exponent into a positive one. Here, we have a negative fraction with a negative integer exponent and we need to work out its value. Which of the following is equal to − 3 4 ?
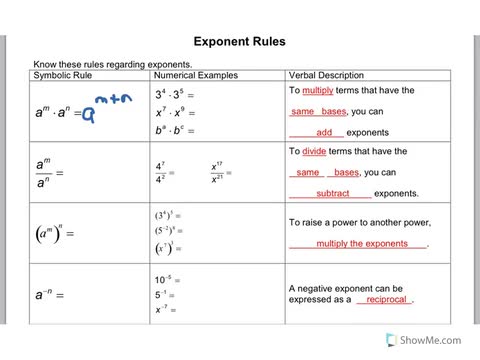
Let us generalize our result.Įxample 3: Evaluating Negative Single-Term Rational Expressions with Negative Integer Exponents Or, using our knowledge of negative exponents, toĪ power of a fraction is therefore just a special case of a power of a product. Note that we could have found the above expression using the rule for multiplying fractions. Using the commutativity of multiplication, we can rewrite the above expression as Of 3 and a repeated multiplication of 1 5 or as a repeated multiplication of 3 and a repeated division ofĥ. This expression is a repeated multiplication of 3 5, which can also be seen as a repeated multiplication We can write 3 5 in expanded form to get Note that since the fraction is within parentheses, the base of the power is the whole fraction, in contrast toģ 5 where only the numerator is a power (it is 3 raised to the fourth power). Then, applying the negative exponent rule 𝑏 = 1 𝑏 , we find that Applied to our expression, we find thatĦ ⋅ 2 = ( 6 ⋅ 2 ) = 1 2. Power of a product of factors is the product of each factor raised to that given power: Note that as an alternative approach, we could have worked backward from the power of a product rule, which states that a given In other words, a negative exponent tells us how many times the base appears in a Recall the negative exponent rule, which tells us that any power is the reciprocal of the power having the same base but an The given expression involves the multiplication of two powers that have a different base, both with a negative exponent. Let us summarize these findings in a table.Įxample 2: Evaluating Powers with Negative ExponentsĮvaluate the following expression: 6 ⋅ 2 . If we carry out the division by 7 once more, we get So, we start seeing a pattern here: every time we divide by 7, the exponent decreases by 1. The number 7 is of course simply 7, but it is useful to write the exponent here, as you will see in the If we perform the same division again on 7 , we get

Let us look at what happens when we divide the power of a number by this number, for instance, 7 divided by 7. To understand the meaning of extending the exponents to negative numbers, So far, we have assumed that the exponent is positive. The question now is whether we could express the result of the previous question, 1 7, as a power of 7. So, here, the eleven 7s in the numerator cancel out withĮleven out of the twelve 7s in the denominator to give 1. Now, we know that one 7 in the numerator cancels out with one 7 in the denominator sinceħ 7 = 1. We have already simplified our expression to

Similarly, we find that theĭenominator is 7 . This is the product rule, which states that The factor 7 and that the factor 7 would appear 3 + 2 + 6 = 1 1 times. By expandingĪll the powers, we see that the numerator would consist of a repeated multiplication of We notice that in this expression, all the powers have the same base: 7. Example 1: Quotient of Powers of the Same Base


 0 kommentar(er)
0 kommentar(er)
